ذرات کوانتومی، دنیایی از شگفتی در دل خود دارند. آمار کوانتومی نشان میدهد دو نوع ذره در عالم داریم، فرمیون و بوزون. اما این همهی ماجرا نیست، ذرات جذاب دیگری به نام انیون ها متولد شده اند که در دنیای دو بعدی زندگی میکنند. آنها نه در دنیای فرمیون ها جای میگیرند و نه در قالب بوزون ها. این ذرات شگفتانگیز، کاربردهای بسیار جذابی دارند. با دیپ لوک همراه باشید…
پرده اول: کوارتیکل یا ذرات کوانتومی
پیش از پدید آمدن مکانیک کوانتوم، فیزیک پایه درگیر دوگانگی عجیبی بود. از طرفی، میدانهای الکتریکی و مغناطیسی را داشتیم که دارای ویژگیهای زیر بودند:
- از قوانین ماکسول پیروی میکردند
- میدان آنها تمام فضا را پر کرده بودند
- پیوسته بودند
از سوی دیگر اتمها را داشتیم که از مکانیک نیوتون پیروی میکردند. اتمها از نظر فضایی اشیایی محدود و در حقیقت، بسیار ریز و مجزا بودند. در قلب این دوگانگی تقابل میان نور و ماده بود، زمینهای که نه تنها دانشمندان، بلکه هنرمندان و عارفان را برای قرنها شیفته خود کرده بود. یکی از افتخارات نظریه کوانتوم این است که این دیدکاه دوگانه ماده را با دیدگاهی یکپارچه جایگزین کرده است. ما یاد گرفتیم از فوتونها میدانها را بسازیم و از الکترونها اتمها را ( البته همراه با دیکر ذرات بنیادی دیگر). هم الکترونها و هم فوتونها با استفاده از ساختاری ریاضیاتی توصیف میشوند. آنها ذره هستند از این نظر که مجزا بوده و دارای خواص قطعی و قابل بازسازی هستند، اما به «ذرات» مکانیک کوانتومی، نمیتوان مکان قطعی در فضا نسبت داد، بلکه نتایج ممکن اندازهگیری مکان آنها، به صورت توزیعی از احتمالات داده میشود. این توزیع، یک میدان فضا پرکن است که تابع موج آن ذره نامیده میشود.
ار نظر مفهومی، ذرات کوانتومی چنان تفاوت قابل توجهی نسبت به اجداد کلاسیکشان دارند که به نظر میرسد باید اسم متفاوتی برای آنها برگزینیم. همانطور که «کیوبیت» کوانتومی متناظر با «بیت» کلاسیک نامگذاری شده است، من هم اینجا عبارت «کوارتیکل» را برای ذره (پارتیکل یا Particle) کوانتومی استفاده میکنم. توجه کنید در این واژه، تاکید روی خاصیت ذرهای است؛ در مقابل خاصیت ذرهای، خاصیت موجی قرار میگیرد که واژه «ویویکل» (wavicle) را برای آن در نظر میگیرم.
پرده دوم: فرمیون ها و بوزون ها
وحدت کوانتومی نور و ماده، در عین راضیکننده بودن، در دامنهی محدودی، واقع شده است. وقتی پا را فراتر از یک تک کوارتیکل گذاشته و به دنبال بررسی رفتار مجموعهای از کوارتیکلهای یکسان میرویم، دوگانگی جدیدی پدید میآید. جهان ذرات کوانتومی به دو قلمرو بزرگ و البته ناسازگار بایکدیگر تقسیم میشود: قلمرو بوزونها که به نام ساتیندرا بوز نامگذاری شده، و قلمرو فرمیونها که به افتخار انریکو فرمی این نام را به خود گرفته است. تمام ذرات، یا بوزن هستند یا فرمیون.
برهمکنش میان بوزونها بسیار متفاوت با فرمیونهاست. ما این اثر را آمار کوانتومی مینامیم. برای آشنایی بیشتر، یک معرفی ساده را ارائه میکنیم.
بوزونها سازشکارند. آنها دوست دارند مانند یکدیگر رفتار کنند. (به زبانی علمیتر:احتمال اینکه بوزونهای همسان، حالت کوانتومی یکسانی را انتخاب کنند، بیشتر است). فوتونها به قلمرو بوزونها تعلق دارند. یک پرتوی لیزر مظهر بوزون بودن است. لیزر شامل تعداد زیادی فوتون از یک طول موج (رنگ) است که در یک راستا حرکت میکنند. لیزر نتیجهی گسیل القایی فوتونهاست.
در مقابل،فرمیونها فردگرا هستند. آنها از برگزیدن یک حالت کوانتومی یکسان، سر باز میزنند، واقعیتی که تحت عنوان اصل طرد پائولی شناخته میشود. الکترونها به قلمروی فرمیونها تعلق دارند و همین، دلیل اصلی وجود جدول تناوبی است (جزییات بیشتر را در کلاس درس کوانتومی هفتم مطالعه کنید). الکترونها با بار منفی، جذب هسته اتمی با بار مثبت میشوند، اما به شیوهی ساده و کارامدی، مانع از فروافتادن یکدیگر روی هسته میشوند. الکترونهای اطراف هسته، ساختار پیچیدهای را میسازند که ریشه جذاب علم شیمی است.
ابرتقارن یک گمانهزنی نظری است که اگر درست باشد، این دو قلمرو (بوزونها و فرمیونها) را با هم آشتی میدهد. بر اساس ابرتقارن، تمام کوارتیکلهای بنیادی، یک جفت یا یک ابرهمزاد در قلمروی مقابل دارند. ابرهمزاد یک بوزون، یک فرمیون است و بالعکس. ابرهمزادها، دارای بار الکتریکی و چند ویژگی یکسان دیگر هستند، اما جرم و اسپین متفاوتی دارند.
ابرتقارن یک توسعهی منطقی و جذاب از فیزیک شناخته شده است و میتواند با ریاضیات زیبایی، پیادهسازی شود. بسیاری از فیزیکدانان، احساس میکنند که ابرتقارن شایسته حقیقت داشتن است، اما علاقه ما مهم نیست چرا که حرف آخر را طبیعت میزند! در حالی که شواهد غیر مستقیم و متقاعد کنندهای برای ابرتقارن وجود دارد، اما تاکنون اثبات مستقیمی برای آن پیدا نشده است. برای این کار، ما باید ابرهمزادها را پیدا کنیم. جستجوی ابرهمزادهای ذرات شناخته شده، دغدغهی بسیاری از محققان برخورد دهنده بزرگ هادرونی (LHC) است. اما متاسفانه تاکنون نتایج، منفی بوده است. با این وجود هنوز امید و ظرفیت زیادی برای اکتشاف ابرهمزادها وجود دارد، چرا که هر چه LHC با انرژی بیشتری کار کند، برخوردهای بیشتری تحلیل خواهند شد و شانس اکتشاف بالا خواهد رفت.
پرده سوم: آمار کوانتومی
واضح است که آمار کوانتومی، یکی از دانشهای بنیادی ما در مورد طبیعت است. از طرفی وقتی درباره وحدت ماده، کنکاش میکنیم، سوالات عمیق دیگری، پیش میآید. برای درک چنین مفاهیم مهمی، ابتدا باید مبانی را خوب بفهمیم. کوانتوم آماری واقعا چیست؟ پاسخ نوین به این پرسش، بسیار عمیق و زیباست. این پاسخ در اواخر دهه ۱۹۷۰، حدود ۵۰ سال پس از بلوغ مکانیک کوانتوم، ظهور کرد و با کارهای پیشروی جان لیناس و ژان میرهیم، توسعه یافت.
به صورت خلاصه، آمار کوانتومی، بازتاب توپولوژی خطوط جهان کوارتیکلهاست. در ادامه، رازها و پیچیدگیهای این جملهی به ظاهر ساده را خواهیم شکافت.
در نظریه کوانتوم، احتمال یک فرایند، با مجذور دامنه تابع موج آن بیان میشود. دامنهها نسبت به احتمالات، بنیادیتر بوده و از قوانین سادهتری پیروی میکنند. از این رو مساله اصلی در دینامیک کوانتومی، محاسبه دامنه تابع موج آرایش ذرات در زمانهای متفاوت است.
در محاسبه دامنه کلی برای دو کوارتیکل تمیزناپذیر که در آغاز در مکانهای A و B هستند و در پایان در C و D، باید سهم تمام حرکات ممکن که مکان آغازین را به مکان نهایی متصل میکند، درنظر بگیریم. این مسیرها، خطوط جهانی کوارتیکلها هستند. حرکتها به دو دسته تقسیم میشوند: اول، کوارتیکلهایی که از نقاط A و B، حرکت را آغاز کرده به ترتیب به نقاط C و D میروند، و دسته دوم به ترتیب به نقاط D و C میروند.

چقدر احتمال دارد دو ذره تمیزناپذیر که از نقاط A و B شروع به حرکت میکنند به نقاط C و D برسند؟ بر اساس قوانین نظریه کوانتوم، ما باید تمام مسیرهای ممکن که به نتیجه پایانی یکسان، منجر میشوند را حساب کنیم. اینجا گزینهها، به دو دسته مجزا تفکیک میشوند: در یک مورد، ذره از A شروع میکند و به C میرسد در حالی که حالت دیگر، به D میرود. چطور میتوان سهم این دو دسته را ترکیب کرد؟ با اضافه یا کم کردن آنها از هم. اضافه کردن آنها به هم بوزونها را به ما میدهد، در حالی که کم کردنشان، فرمیونها را بدست میدهد.
از آنجایی که کوارتیکلها تمیزناپذیرند (مانند هم هستند)، نتیجه نهایی (یعنی دو کوارتیکل در نقاط C و D) در هردو مورد، یکسان خواهد بود. با این وجود، هر جفت خطوط جهانی، توپولوژی مجزایی دارند، در واقع آنها از نظر توپولوژی متفاوت هستند. ما به قاعدهای نیاز داریم که بگوید چگونه میتوانیم سهم این دو دسته را ترکیب کنیم. دو راه ممکن که از نظر ریاضی باهم سازگارند وجود دارد. ما میتوانیم آنها را هم جمع کنیم، یا از هم کم کنیم. گزینه «جمع»، بوزونها؛ و گزینه «تفریق»، فرمیونها را میدهد. میتوان تمام ویژگیهای مشخصهی بوزونها و فرمیونها را از این قواعد بنیادی استنتاج کرد. این یک دستاورد ذهنی فوقالعاده است که از دنبال کردن ویژگیهای مهم ماده به ذات ذرات (یعنی تمیزناپذیری) و توپولوژی حرکت در فضا زمان، پی بردهایم.
پرده چهارم: تولد انیون ها
دستاورد واقعی زمانی حاصل میشود که ما این درک بنیادی را برای کشف چیزهای جدید استفاده کنیم. شگفتانگیزترین کاربرد این درک عمیقتر ما از آمار کوانتومی، زمانی خود را نشان میدهدکه کوارتیکلهایی را درنظر بگیریم که در دو بعد زندگی میکنند. شاید تعجبآور باشد، در یک دنیای دوبعدی، توپولوژی جفت خطوط جهانی، بسیار غنیتر از دنیای سهبعدی (یا ابعاد بالاتر از سه بعد) است! دلیل این حقیقت جذاب، ارتباط تنگاتنگی با نظریه گره دارد.
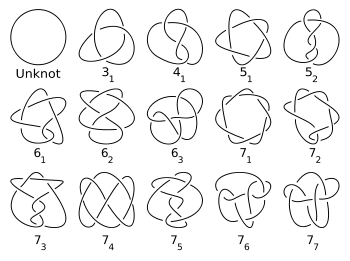
نظریه گره در سه بعد فضا، مسئلهای دقیق و پیچیده است، اما در چهار بعد فضا، بسیار ساده است: تمامی گرهها میتوانند کاملا باز شوند. یک گره برای ریاضیدانان، تنها یک منحنی پیوسته در فضاست. تصور کنید تمام نقاط روی این منحنی درهم پیچیده را با اعدادی بین صفر و یک برچسب بزنید، بهطوری که صفر و یک نمایانگر یک نقطه یکسان باشند، اکنون یک دایره بکشید و همین کار را بکنید.
برای باز کردن یک گره کافیست نقاط روی گره را به نقاط روی دایره که با شمارههای متناظر برچسب خوردهاند، منطبق کنید. البته ممکن است اینکار کمی دشوار باشد، مخصوصا در مورد قسمتهایی از منحنی که یکدیگر را قطع میکنند، اما در چهار بعد، ما همیشه میتوانیم دو رشته را از پس هم بگذارنیم.
شاید تجسم مستقیم این کار، برایتان دشوار باشد، اما با ترفندی ساده میتوانید درکش کنید. اجازه دهید موقعیت در یک بعد اضافه را با مقدار یک دمای فرضی نشان دهیم. اگر تقاطع مورد نظر در نقطهای رخ دهد که دمای رشتهها متفاوت است، یک تقاطع واقعی نخواهد بود، زیرا رشتهها در بعد اضافی، مکان متفاوتی دارند و اگر دماها یکسان بود تنها لازم است که یک انتقال موقت به بعد اضافی انجام دهیم، یعنی یکی از رشتهها را گرم کنیم، آن را جلو ببریم (در ابعاد معمول)، و سپس دوباره سردش کنیم تا از تقاطع، به سلامت، رد شویم!
خطوط جهانی کوارتیکلهایی که در فضای سهبعدی حرکت میکنند، یک رشته را در فضا-زمان چهاربعدی شکل میدهند. از این رو، همانگونه که دیدیم، آنها نمیتوانند واقعا در هم پیجیده شوند. توپولوژی آنها، کاهش مییابد تا مبادلهها را دنبال کند. از سوی دیگر، خطوط جهانی کوارتیکلهایی که حرکتشان در یک فضای دوبعدی مقید شده، رشتهای در فضا-زمان سهبعدی را شکل میدهد. رشتهها در فضای سه بعدی قطعا میتوانند درهم پیچیده شوند، کسانی که موهایشان را میبافند، به خوبی این حقیقت را درک میکنند.
با چنین توپولوژی غنیتری، گستره متنوعتری از احتمالات برای جمع کردن سهمهای خطوط جهانی وجود دارد، به عبارت دیگر، احتمالات بیشتری برای آمار کوانتومی وجود دارد، و بدین ترتیب نوع تازهای از ذرات، غیر از بوزونها و فرمیونها ظاهر خواهند شد. من واژه انیون (Anyon) را برای کوراتیکلهایی که حرکتشان در دو بعد مقید شده، و نه بوزون هستند و نه فرمیون، برگزیدهام. انیون ها باید از قواعد کاملا ساختارمند ریاضی تبعیت کنند. جالب است که هنوز به جای دو تا، ما تعداد بیشماری احتمالات سازگار برای آنها پیدا میکنیم.

در تصویر بالا، انیون های درهم پیچیده، تبادل یک ذره پس از تبادل دیگر، رخ میدهد. در سه بعد فضا (و یک بعد زمان)، این گونه تبادل دوگانهی جفت مسیر را میتوان به یک جفت بدون تبادل، باز کرد. این مساله، یک شرط سازگاری را بر ضریب همراه تبادل تحمیل میکند: وقتی ما آن را دو بار اعمال میکنیم، باید به همان جایی که اول بودیم، برگردیم. به همین خاطر، فقط ضرایب تبادل سازگار، ۱ و ۱- هستند که به ترتیب متناظر با بوزونها و فرمیونها هستند. با این حال، در دو بعد فضا (به علاوه یک بعد زمان)، چرخش یک مسیر حول دیگری را نمیتوان با هیچ حرکت پیوستهای خنثی کرد. در نتیجه، شرط سازگاری از بین میرود و در چنین حالتی، آنیونها به عنوان یک احتمال جدید، متولد میشوند.
از آنجایی که قواعد رفتار انیون ها به حرکت کوارتیکلها در زمان حساس است، پس انیون ها حافظه دارند. به زبان دقیقتر: از آنجایی که دامنه تحول انیون ها بسته به اینکه خطوط جهانی آنها چگونه در طول زمان، درهم پیچیده میشوند، متفاوت خواهد بود، مقدار دامنه، نشاندهنده حرکت نسبی آنهاست. در ادامه خواهیم دید که توانایی حافظه انیون ها میتواند منجر به تکنولوژیهای مهمی شود.
پرده پنجم: انیون های شگفتانگیز و کاربردهای شگفتانگیزتر!
آیا انیون ها خارج از تصورات نظریه پردازان وجود دارند؟ پاسخ سریع ما شاید این باشد: حداقل در جهان ما نه، زیرا در جهان ما، فضا، سهبعدی است. اما این نتیجهگیری در مقابل خلاقیت ما و طبیعت، کم میآورد. حقیقت این است که جهانهای دوبعدی در اطرف ما هستند و ما آنها را سطوح، نوارها، غشاها و سطوح مشترک مینامیم. آنها میتوانند از پیچیده شدن جهان سهبعدی ما پدید آیند، اما آنها زندگی خاص خودشان را دارند! به عبارتی، برخی از این اشیای دوبعدی به شکل موثری انرژی را درون خودشان به دام میاندازند و اگر کسی مزاحم آنها نشده و جهانشان را مختل نکند، زندگی خاص خود را ادامه خواهند داد. البته ویژگیهای این جهانها به این بستگی دارد که از چه چیزی ساخته شدهاند و الگوی ساختاریشان چیست. اخیرا، علاقه به مواد دوبعدی که الکترونهایشان شدیدا درهم تنیده شده، افزایش یافته است. برای تعریف دقیق و فنی عبارت «شدیدا درهم تنیده»، باید مفاهیم عمیق ریاضیات نظریه کوانتوم را استفاده کنیم. در مورد انیون ها تقریبا با چنین موقعیتی مواجه هستیم، یعنی برای توضیح رفتار انیون ها باید به عمیقترین مفاهیم کوانتومی رجوع کنیم.
وقتی الکترونها یک پیوند کوالانسی شکل میدهند، دیگر نمیتوانند بهطور مستقل حرکت کنند؛ میتوان گفت آنها در جایشان یخ زده و چیزی شبیه یک جامد را تشکیل میدهند. افت و خیزهای کوانتومی میتوانند باعث تصعید این جامد شده و موادی را تولید کند که در آن الکترونها، آزادانه حرکت کنند، یعنی نوعی گاز الکترون. این بیان شاید ناپخته باشد، اما راه بسیار مفیدی برای توصیف وضعیت الکترون در فلزات است. ما میتوانیم حالات بینابینی را هم تصور کنیم که الکترونها نه کاملا مقید هستند و نه مستقل و چیزی مانند مایع را تشکیل میدهند. این مایعهای عجیب که به خاطر افت و خیزهای کوانتومی، ذوب شدهاند (و نه به خاطر گرما)، بسیار جذاب هستند. در این حالت، الکترونها منظم میمانند، اما دیگر کاملا سفت و محکم در جایشان نیستند. نظمی که از آن صحبت میکنیم، همان همبستگی نامحسوس، یعنی درهم تنیدگی کوانتومی است.
نقصها در آرایش منظم این مایعها، بسیار شبیه به ناخالصیها در مایعات معمولی رفتار میکنند. آنها یک آرایش پایدار را تشکیل میدهند که ساختار اساسی خود را حتی در زمان حرکت حفظ میکند. بدین ترتیب، به نوعی، با یک ذره ظهوریافته یا از آنجا که ما با مایعهای کوانتومی سروکار داریم بهتر است بگوییم با یک کوارتیکل ظهوریافته سروکار داریم. این کوراتیکلهای ظهوریافته با الکترونهای منفرد تفاوت دارند و ویژگیهای کاملا متفاوتی نسبت به الکترونها دارند.
«هر چیزی که ممنوع نیست، اجباری است». این عبارت به یادماندنی از رمان «پادشاه گذشته و پادشاه آینده» نوشته تی.اچ.وایت، قاعده مهمی در رفتار کوانتومی را نشان میدهد: فعالیت خودبهخودی سیستمهای کوانتومی، همهی احتمالات سازگار را بدست میدهد. برای من، این یک قاعده الهام بخش در کاوش نظری هم بوده: طبیعت با سخاوتش باعث میشود تا مواد، تمام احتمالات سازگار با نظریه را بدست دهند. با تکیه بر این قاعده، من تلاش کردم تا آنچه که ریچارد فاینمن، تصور با straitjacket (ژاکت ویژه خفت کردن دیوانگان) نامیده بود را تمرین کنم، با انتظار اینکه:
اگر چیزی را تصور کنید، آن (به صورت فیزیکی) اتفاق خواهد افتاد
حداقل میدانم که در مورد آنیونها، جمله بالا، ثابت شده است. فیزیکدانان اکنون چند مایع کوانتومی دوبعدی میشناسند که کوارتیکلهای ظهوریافته آنها نه بوزون هستند نه فرمیون، بلکه بیشتر گونههای متفاوتی از انیون ها هستند.
اولین مورد در حوزه شگفتی انگیزی از فیزیک به نام اثر کوانتومی کسری هال (FQHE) پیدا شد. FQHE، حالتی از ماده بوده و هنگامی پیش میآید که الکترونهای محبوس در یک لایه دوبعدی (معمولا در سطح تماس دو نیمه رسانا) به دماهای بسیار پایین بروند و در معرض یک میدان مغناطیسی بسیار بزرگ قرار گیرند. در این شرایط، با تغییر چگالی و میدان مغناطیسی، الکترونها یک دسته بزرگ از مایعات کوانتومی مرتبط اما مجزا و با ویژگیهای قابل توجه را میسازند.
کوارتیکلهای ظهوریافته در این مایعات، معمولا حامل بار الکتریکی هستند که کسری از بار الکتریکی الکترون است و از آمار کوانتومی پیروی میکنند که کسری از آمار فرمیونهاست! مثلا در قویترین حالت FQHE، کوارتیکلها، یک سوم بار الکترون را دارند. به طور کلی، کوارتیکلها مانند یک سوم یک الکترون رفتار میکنند، در واقع، یک الکترون، به سه عدد از این کوارتیکلها شکافته میشود. به کمک شواهد تجربی میتوان پیشبینی کرد که این کوارتیکلها، همان انیون ها باشند که یک سوم آمار فرمیونی را به نمایش میگذارند. به بیان ریاضی، دامنهی این کوارتیکلها، در ریشه سوم ۱- ضرب میشود.
نظریه FQHE، بسیار توسعه یافته و پیشبینیهای بسیار موفق در رابطه با مایع های کوانتومی مشاهدهشده کرده است. از آنجا که کوارتیکلهای انیونی، ویژگی محوری این نظریه هستند، اکثر نظریه پردازان، شک ندارند که انیون در طبیعت وجود دارد و همین دلیل، به دقت مایعهای FQHE را زیر نظر دارند. مطالعات عددی نیز این باور را تقویت میکند. با این وجود متاسفانه رسیدن به اثبات تجربی، به چند دلیل عملی، بسیار دشوار است، اما محققان کار روی این مساله را ادامه خواهند داد چرا که آنها به شکل وسوسهانگیزی به موفقیت نزدیک هستند.
دسته بسیار جدیدی از مایعهای کوانتومی که مایع های اسپین کوانتومی نامیده میشوند شناسایی شدهاند. در این مواد، الکترونها حرکت نمیکنند، اما اسپین آنها، تغییر میکند. مایعهای اسپین در میانهی گسترهی آهنرباهای عادی (که در آنها، راستای اسپین کاملا هم راستا و ثابت است) و پارامگنتها و دیامگنتها (که در آنها راستای اسپینها تقریبا به صورت کامل از یکدیگر مستقل هستند) قرار میگیرند. مدلهای نظری مایعهای دوبعدی نشان میدهد که بسیاری از آنها کوارتیکلهای انیونی را تایید میکنند. مشکلاتی که بر سر راه مطالعهی انیون ها در FQHE وجود دارد، در در مایعهای اسپین کمتر دیده میشود، پس میتوان منتظر پیشرفت سریع بود.
اخیرا فعالیتهای قابل توجهی در مهندسی سیستمهای انیون مصنوعی صورت گرفته است. به یاد داشته باشید که ویژگی اساسی انیون ها که آنها را از کوارتیکلهای شناخته شده، متمایز میکند حافظهی آنهاست. سیستمی متشکل از انیون های فراوان، یک حافظه بزرگ را میسازد که میتواند به عنوان بستری برای محاسبات کامپیوتری مورد استفاده قرار گیرد. این محاسبه کوانتومی توپولوژیکی، یکی از راههای محتمل برای ساخت کامپیوترهای کوانتومی است. مایکروسافت در حال سرمایهگذاری عمدهای در این زمینه است. اگر محاسبه توپولوژیکی نهایتا منجر به کامپیوترهای کوانتومی شود، آن وقت، میتوانیم مدعی شویم تواناترین هوش مصنوعی در مواد دوبعدی زندگی میکند که در سیستمهای انیونی مجسم میشوند، پس میتوانیم چشم به راه ظهور ابرمغزها باشیم…





گفتگو۳ دیدگاه
مقاله بسیار بسیار خوبی بود امیدوارم این کار تکرار شود اگر در زمینه پراکندگی پرتو اتمی و مولکولی هم مثالهای مو جود است قرار دهید
بسیار ارزشمند ….سپاس گذار
متشکرم