پس از شش قسمت از مجموعه مقالات کلاس درس کوانتومی، در قسمت هفتم به سراغ تقارن تابع موج می رویم. مفهوم تقارن در دنیای کوانتومی با معنی آن در دنیای روزمره و ماکروسکوپی، بسیار متفاوت است، بنابراین سناریوی امروز را با توضیح تقارن تابع موج آغاز می کنیم و در ادامه ی داستان به سراغ دو مفهوم برآمده از آن، یعنی فرمیون و بوزون می رویم. با دیپ لوک همراه باشید…
پرده ی اول: تقارن تابع موج
وقتی اشیای دنیای ماکروسکوپی را توصیف می کنیم، اغلب از کلماتی مانند “یکسان” یا “همان” استفاده می کنیم. مثلا می توانیم ادعا کنیم که دو گوشی آیفون ۶ اس، یکسان هستند. اما این فقط یک نگاه خام است! اگرچه در نگاه اول، هیچ تفاوتی بین این دو گوشی، احساس نمی کنیم، اما آنها واقعا یکسان نیستند و در مقیاس ملکولی با یکدیگر تفاوت دارند. از طرفی، در دنیای ماکروسکوپی، می توانیم این دو گوشی به اصطلاح یکسان را از یکدیگر تفکیک کنیم، مثلا می توانیم یکی را با رنگ آبی و دیگری را با رنگ قرمز، علامت گذاری کنیم. اما در جهان میکروسکوپی، کلمات “همسان” یا “قابل تشخیص”، معنای کاملا متفاوتی دارند. هر دو ذره ی کوانتومی (مانند الکترون، پروتون، فوتون و …) کاملا با یکدیگر یکسان هستند و هیچ راهی برای جدا کردن و تفکیک آنها وجود ندارد، چرا که در این مورد، نمی توانیم، یکی را علامتگذاری کنیم. در واقع، علامت گذاری یک الکترون با رنگ های متفاوت، غیرممکن است، زیرا در جهان کوانتومی، حتی رنگ هم معنی ندارد!
اجازه دهید برای درک بهتر این موضوع، به سراغ توپ های رنگی دوران کودکی برویم. فرض کنید یک توپ آبی و یک توپ قرمز و دو سبد دارید و میخواهید آنها را در دو سبد توزیع کنید. چند راه برای توزیع آنها، وجود دارد؟ شکل زیر، چهار حالت ممکن برای توزیع دو توپ در دو سبد را نشان می دهد.
طبق شکل بالا، با احتمال ۵۰ درصد، دو توپ را درکنار هم در یک سبد خواهید دید (۲۵ درصد دو توپ در سبد سمت راست و به احتمال ۲۵ درصد هر دو توپ در سبد سمت چپ) و به احتمال ۵۰ درصد هم دو توپ در سبدهای جداگانه خواهند بود (۲۵ درصد توپ قرمز در سبد سمت راست و به احتمال ۲۵ درصد توپ قرمز در سبد سمت چپ). اما صبر کنید! این ها فقط توپ های ماکروسکوپی هستند در حالیکه ما درباره ی ذرات کوانتومی صحبت می کنیم، پس اجازه دهید، داستان را با توپ های کوانتومی ادامه دهیم. توپ های کوانتومی می توانند در یک برهم نهی از حالت های کوانتومی قرار داشته باشند. حالا دوباره فرض کنید میخواهیم دو توپ را در دو سبد توزیع کنیم. باز هم با چهار حالت به شکل زیر مواجه می شویم:
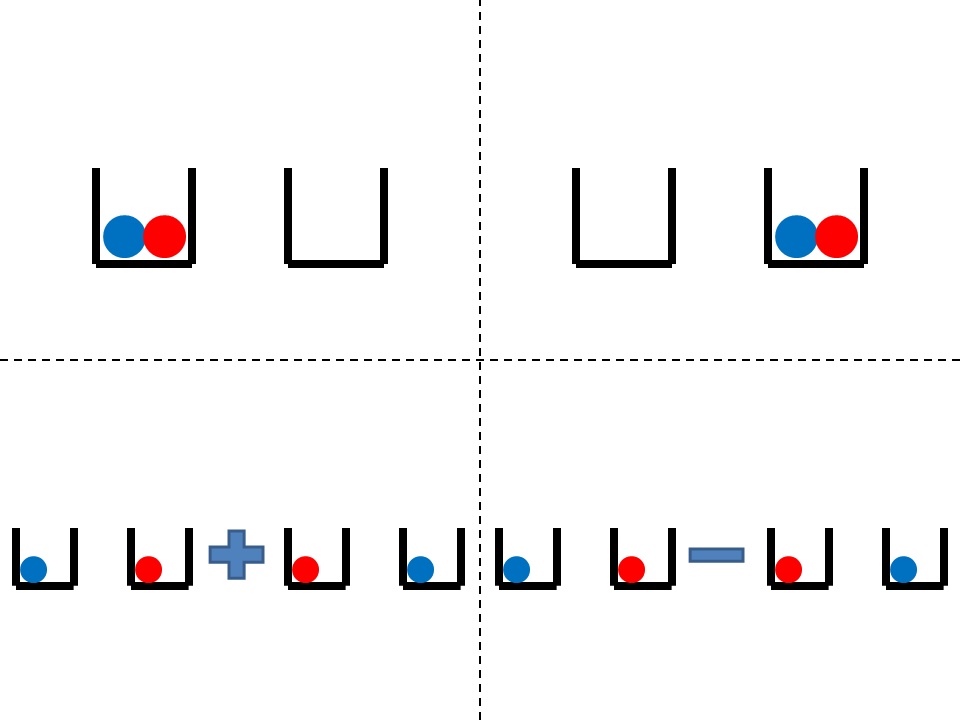
پرده ی دوم: فرمیون و بوزون
فیزیکدانان علاقمندند جهان را به دو دسته تقسیم کنند:ماده ی معمولی و ماده ی تاریک، رسانا و نارسانا، لپتون و کوارک ها. برخی از این دسته بندی ها فقط برای راحتی و به طور اختیاری انجام می شوند، در حالیکه برخی، بنیان طبیعت را توصیف می کنند. یکی از این دسته بندی های بنیادی، بوزون ها و فرمیون ها هستند، مفاهیمی که بدون آنها، گیتی به شکلی که امروز میشناسیم، وجود نداشت!
راه های زیادی برای تعریف تفاوت بین این دو مفهوم وجود دارد: فیزیکدانان متخصص ذرات بنیادی، بوزون ها را به عنوان ذرات حامل نیرو و فرمیون ها را به عنوان ذرات ماده در نظر می گیرند، اما این دو مفهوم، به طور استاندارد بر اساس اسپین، تعریف می شوند. فرمیون ها دارای اسپین نیمه صحیح و بوزون ها دارای اسپین صحیح هستند. همین تفاوت به نظر ساده، اثرات بسیار عمیقی بر ساختار کائنات گذاشته است. فرمیون ها درست مانند آدم های منزوی و گوشه گیری هستند که به هیچ وجه، جمع شدن در کنار یکدیگر را دوست ندارند، در حالیکه بوزون ها، موجوداتی بسیار اجتماعی هستند و دوست دارند همیشه با یکدیگر باشند.
حالا بهتر است تفاوت فرمیون و بوزون را در بحث تقارن تابع موج نشان دهیم. در واقع هر یک از سبدها در شکل ۱ و ۲، نقش یک تابع موج ψ را بازی می کند. با این حساب چهار حالت شکل ۲ را با استفاده از تابع موج می توان به شکل زیر نمایش داد:
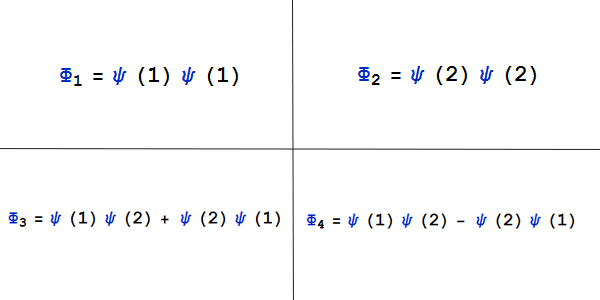
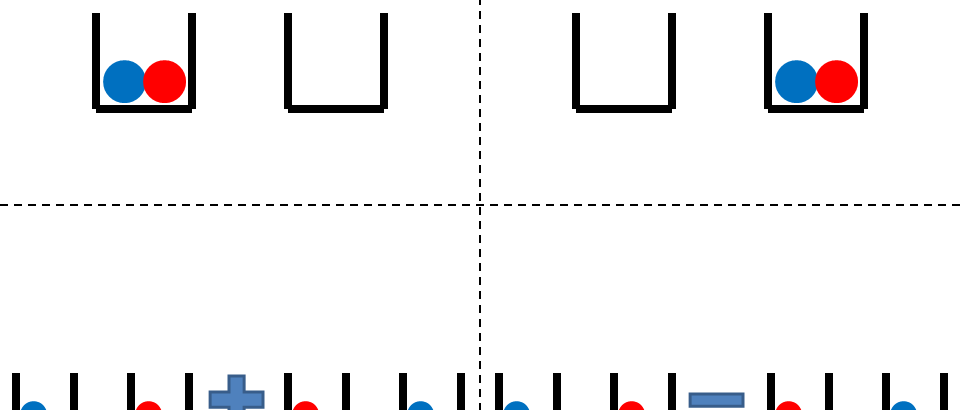
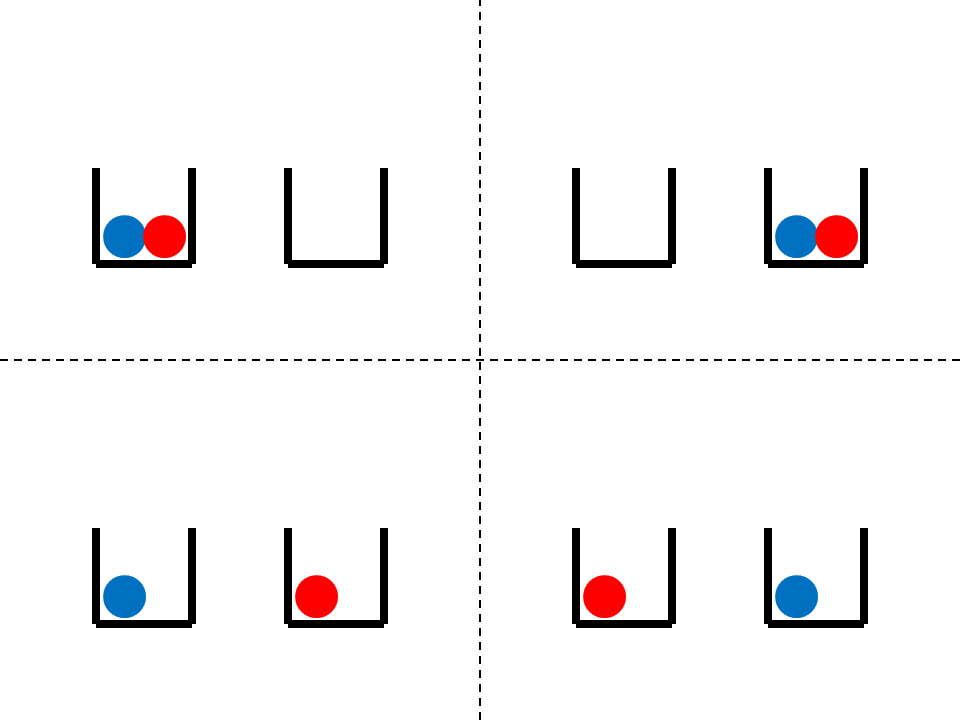
در شرط بالا، تابع موج متقارن به تابعی گفته می شود که با جا به جا کردن ذرات (یعنی جابه جاکردن ۱ و ۲های داخل پرانتزها)، همان تابع اولیه را بدهد و تابع موج پادمتقارن به تابعی گفته می شود که در صورت جابجایی ذرات، به منفی تابع اولیه تبدیل شود. اجازه دهید این شرط را در هر چهار تابع Φ آزمایش کنیم. اگر جای دو ذره را در Φ۱ و Φ۲ عوض کنیم، باز به همان تابع موج اولیه میرسیم، بنابراین این دو تابع موج، متقارن هستند. در مورد دو تابع Φ۳ و Φ۴ طبق شکل زیر اگر جای دو ذره را عوض کنیم، به ترتیب به Φ۳ و Φ۴- می رسیم. در نتیجه Φ۳ متقارن و Φ۴ پاد متقارن است.
در نتیجه سه تابع موج Φ۲، Φ۱ و Φ۳ متقارن بوده و می توانند به عنوان تابع موج بوزون ها استفاده شوند، در حالیکه برای فرمیون ها فقط یک انتخاب داشته و تنها تابع موج Φ۴ را می توانیم استفاده کنیم. حالا می توانیم دلیل اجتماعی بودن بوزون ها و گوشه گیر بودن فرمیون ها را درک کنیم: تنها تابع موجی که برای فرمیون ها، مجاز است، حالتی است که دو توپ جدا از یکدیگر هستند و در مقابل، از بین سه حالتی که برای بوزون ها مجاز است، دو حالت آن مربوط به زمانی است که توپ ها در کنار هم و در یک سبد قرار گرفته اند. بنابراین، شاید فرمیون ها زیاد هم گوشه گیر نباشند، چرا که آنها چاره ی دیگری ندارند! نکته ای که باید به آن توجه کنیم این است که اجتماعی یا منزوی بودن بوزون ها و فرمیون ها ناشی از نیروهای جاذبه ای یا دافعه ای بین آنها نیست، بلکه مستقیما ناشی از شرط متقارن یا پاد متقارن بودن تابع موج آنهاست و بنابراین بیش از آنکه یک واقعیت فیزیکی باشد، یک شرط ریاضی است. ساتیندرا بوز، فیزیکدان بنگالی، قوانین حاکم بر بوزون ها را بدست آورد و واژه ی “بوزون” نیز به افتخار او گذاشته شده است. انریکو فرمی نیز کسی بود که قوانین ذرات فرمیون مانند را استخراج کرد و وجه تسمیه ی “فرمیون” نیز همین است.

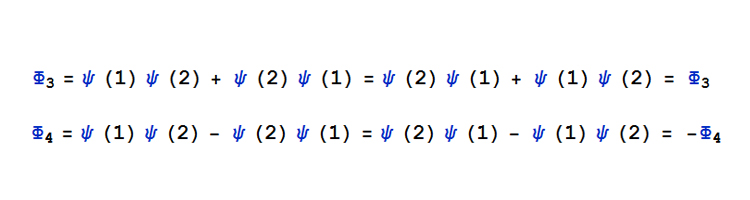

گفتگو۲۵ دیدگاه
واقعا ممنونم از آموزش های بسیار زیبا و دقیقتون که نشانه از درک عمیق شما بر مطلب و علاقه به انتشار علم دارد
ممنون میشم اگه جلسات آموزشیتونو زود تر بروز کنین و سریع تر مطالب رو پیش ببرین تا بنده و دیگر علاقه مندان استفاده بیشتر و بهتری ببریم
با عرض خسته نباشید و تشکر فراوان
سپاسگزارم دوست خوبم از اظهار لطفتون. متاسفانه به علت کمبود وقت، جلسات کمی به تعویق می افتاد، اما خوشبختانه چند جلسه آینده، نیمه آمادس و سعی میکنم در اولین فرصت منتشر کنم.
سلام ممنونم از مطالب ارزشمندتون
براتون مرتب دعا می کنم – بشدت منتظر بقیه مطالبتون هستم .
ممنون از پست هاتون قضیه کوانتوم مقداری عجیب مثلا این که یک الکترون در دو جا باشه و.. انگار شما شب تو زمین بخوابی تو مریخ بیدار شی البته این پدیده به علت بالای الکترون ها اتفاق نمی افته یادمه حتی کار این احتمالات به جایی رسید که خود اینیشتن گفت خدا تاس بازی نمی کنه راستی خانم ریاحی کتابی که از پایه فیزیک کوانتوم بررسی کنه می شه معرفی کنید؟
دوستان زیادی درخواست کتابهای مقدماتی و پایه ای برای مطالعه کوانتوم کردند، سعی می کنم به زودی، در یک پست، چند کتاب خوب رو معرفی کنم
سلام
ممنون ، از مطالب ارائه شده استفاده کردم. بطور ساده چگونگی حل و بدست آوردن معادلات ویژه حالات و مقادیر بوزون ها را کجا مطالعه کنم؟
با آرزوی سلامتی و موفقیت برای شما
دوست خوبم شما می تونید در کتاب شیمی کوانتومی زابو که در دانلود کده (لینک زیر) قرار داده شده، این اطلاعات رو پیدا کنید
http://www.deeplook.ir/shop/quantum-chemistry/%D8%B4%DB%8C%D9%85%DB%8C-%DA%A9%D9%88%D8%A7%D9%86%D8%AA%D9%88%D9%85%DB%8C-%D9%85%D8%AF%D8%B1%D9%86-%D8%B2%D8%A7%D8%A8%D9%88/
با سلام و آرزوی موفقیت برای شما
واقعا از زحمات شما در بررسی و توضیح بسیار زیبا و عمیق مطالب تشکر می کنیم
سپاسگزارم دوست عزیز. خوشحالم مطالب موردنظرتون قرار گرفته
سلام من علاقه به محاسبات کوانتمی یا شبه کوانتمی هستم یعنی دوست دارم نتایجم با آزمایش تا حدودی قابل مقایسه باشه. اگه ممکنه راهنماییم کنید. البته تا حدودی محاسبات کوانتمی در دمای صفر(حل معادله شرودینگر) را انجام داده ام . ممنون از مطالب مفهومی کوانتومی شما
سلام خانم ریاحی این همه علاقه شما به علم و از آن مهمتر انتشار آن به زبان ساده و جذاب برای علاقمند کردن دیگران قابل تحسین است. فقط چند تا مشکل تو این پست بود که خواستم بهتون اطلاع بدم.در پرده سوم این جمله “ذرات با اسپین صحیح از آمار بوز-اینشتین (پادمتقارن بودن تابع موج) و ذراتی با اسپین نیمه صحیح از آمار فرمی-دیراک (متقارن بودن تابع موج) پیروی می کنند.” ، داخل پرانتزها جابجا نوشته شده. و دوتا کتابی که در این قسمت معرفی کردینو دانلود کردم، چرا هردوتا مثل هم (کتاب شوارتز) بود؟!
از اظهار لطف شما بسیار سپاسگزارم. در مورد اشتباهات، عذرخواهی میکنم و از حسن دقت شما، کمال تشکر رو دارم. هم اشباهات اصلاح شد و هم لینک کتابها تصحیح شد.
با سلام و وقت بخیر.بیانتون خیلی زیبا بود ولی ای کاش پخته تر بود یکم. من دنبال مفهومی که توی کتابای درسی نباشه میگشتم ولی شما همونا رو گذاشتید. در واقعا فقط بیان عوض شده.
خب اینکه بدیهیه! مفاهیم، یکی هستند، فقط بیان عوض میشه! اگه یه مفهوم دیگه بگیم که دیگه میشه یه موضوع دیگه!!!
سلام علیکم ، خانم ریاحی گرامی ،بسیار عالی،واقعا استفاده کردم و لذت بردم؛ممنونم. دیدگاه علمیتون به بنده نزدیک هست .اینکه مسائل اینچنین مشکل رو به زیبایی و سادگی بیان میکنید .نشان از هوش بالا و درک عمیق شماست که این نشان از تحصیل علم برای پی بردن به عمق مطالب و پی بردن به پیچیدگی های آن هست . نه صرفا گرفتن مدرک . این بسیار کمیاب شده و بسیار ستودنیست. باز هم ممنونم.(دانشجوی ارشد فیزیک)
سپاسگزارم از اظهار لطفتون دوست خوبم و خوشحالم دیپ لوک مورد توجهتون قرار گرفته
خواهش میکنم ، بزرگوارین.بسیار ممنونم از توجه شما به پیامم و تواضع و صمیمتتان در پاسخ به بنده حقیر انشاا… سلامت باشین.خوشحالم هر چند تصادفی با دیپ لوک برخورد و آشنا شدم.از زحمات شما که علارقم گرفتاری های تحصیلی فراوان در دوره دکترا باز هم وقت میگذارین و این کیفیت بالا رو در کارتون حفظ میکنید.تشکر فراوان میکنم.
سپاسگزارم
با عرض سلام
من ی سوال در مورد بوزون ها دارم
وقتی خواسیم بوزون ها را بررسی کنیم و خواص ترمودینامیکیشونا را بدست بیاریم تو فضای سه بعدی بررسی کردیم
حالا چرا در فضای یک بعدی و دو بعدی نمیشه؟
ممنونم
سلام ببخشید می شه همیلتون توابع موج اسپینی کربن رو بفرمایید
با سلام و عرض ادب
میخواستم بگم که اگر میشه در مطالب توضیح بیشتری در باره اصل ها و معادلات بدید
سلام خانم دکتر
چطور میشه تشخیص داد که به عنوان مثال o 16 یا Br 79 بوزون یا فرمیون هستند
ممنون
سلام
بسیار مفید و آموزنده بود.
براتون امکان داره برام درمورد بهنجارش توابع موج توضیح بدید و اینکه چرا باید توابع موج رو بهنجار کنیم و روش بهنجار کردن توابع موج رو هم لطف کنید و بفرمائید؟
ممنونم.
احتمال یافتن ذره در مکانیک کوانتومی از طریق مربعسازی تابع موج و سپس انتگرالگیری آن روی تمام فضا بدست میاد. ما میدونیم که احتمال باید بین مقادیری بین ۰ تا ۱ داشته باشه (که صفر یعنی یک نتیجهی غیرممکن و یک یعنی نتیجهی قطعی)، بنابراین انتگرال مربع تابع موج روی کل فضا، باید برابر یک باشه، یعنی ذره حتما جایی در فضا وجود داشته باشه و این یعنی باید حاصل این انتگرال باید برابر یک باشه.
سلام. برای درست بودن نتایج باید یک اندیس اضافی هم بعنوان شماره ذرات به توابع موج اضافه شه و الا شما هرجور حساب کنید هر چهار حالت متقارن میشن-